Type Analysis: Basic Concepts

In most programming languages, objects are declared in one part of the program and used in others. We’ve already mentioned that scope analysis is the calculation of the function that assigns to each use of an object the definition that applies to it.

Type analysis aims to ensure that the use of defined objects is correct: that is, that their use adheres to the semantics of their definition; for example:

• that an array of integers is not called as a function or
• that a function is not attempted to be incremented or
• that the value returned by a function is of the nature described in its definition.

Type Expressions

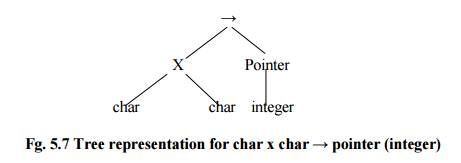
An appropriate way to represent types within a compiler is by using a language of type expressions.

A language of type expressions should describe the types of the source language in a clear and simple manner. Do not confuse this language with the sub-language of the source language that consists of declarations or definitions.

They don’t have to be the same. The compiler translates type declarations into type expressions.

The language of type expressions is the internal representation that the compiler has of these declarations and depends on the compiler.

Type System

A Type System of a language/compiler is the set of language rules that allows assigning type expressions to instances of use of program objects.

While the type system is a property of the language, it is not uncommon for compilers to introduce modifications to the language’s type system.

For example, in Pascal, the type of an array includes the array indices. This and Pascal’s type equivalence rules severely limited the genericity of functions in Pascal. For this reason, some Pascal compilers allowed compatibility of types between arrays of different sizes and different index sets in a function call. Unfortunately, the way they did this differed from compiler to compiler.

Type Checker

A Type Checker verifies that the use of objects in usage constructs adheres to what is specified in their declarations or definitions according to the rules specified by the type system.

Static Typing and Dynamic Typing

A programming language has static typing if its type checking occurs at compile time without having to check equivalences at runtime.

A programming language has dynamic typing if the language performs type checks at runtime.

In a dynamic type system, types are usually associated with values not with variables.

Strong Typing and Weak Typing

Although the meaning of the terms Strongly Typed and its opposite Weakly Typed vary with authors, there seems to be consensus that languages with strong typing usually have some of these characteristics:

• Compile-time checking of violations of restrictions imposed by the type system. The compiler ensures that for any operations the operands have valid types.
• Any operation on invalid types is rejected either at compile time or runtime.
• Some authors consider that the term implies disabling any implicit type conversion. If the programmer wants a conversion, they must explicitly specify it.
• The absence of ways to bypass the type system.
• That the type of a data object does not vary during the life of the object. For example, an instance of a class cannot have its class altered during execution.

Sobrecarga, Polimorfismo e Inferencia de Tipos

En algunos lenguajes se permite la sobrecarga de funciones. Así es posible tener dos funciones llamadas min:

  int min(int a, int b) {       string min(string a, string b) {     
       if (a < b) return a;          if (strcmp(a, b) < 0) return a; 
       return b;                     return b;                       
  }                             }                                 

A la hora de evaluar el tipo de las expresiones es el contexto de la llamada el que determina el tipo de la expresión:

    float x,y;
    int a,b;
    string c,d;
 
    u = min(x,y); /* Puede que correcto: x e y seran truncados a enteros. Tipo entero */
    v = min(a,b); /* Correcto: Tipo devuelto es entero */
    w = min(c,d); /* Correcto: Tipo devuelto es string */
    t = min(x,c); /* Error */

¿Como afecta al análisis de ámbito la sobrecarga de operadores?

Overloading, Polymorphism, and Type Inference

In some languages, function overloading is allowed. Thus, it is possible to have two functions named min:

  int min(int a, int b) {       string min(string a, string b) {     
       if (a < b) return a;          if (strcmp(a, b) < 0) return a; 
       return b;                     return b;                       
  }                             }                                 

When evaluating the type of expressions, it is the context of the call that determines the type of the expression:

    float x,y;
    int a,b;
    string c,d;
 
    u = min(x,y); /* May be correct: x and y will be truncated to integers. Integer type */
    v = min(a,b); /* Correct: Returned type is integer */
    w = min(c,d); /* Correct: Returned type is string */
    t = min(x,c); /* Error */

Think 🤔: How does function overloading affect scope analysis?

Type Inference

Type inference refers to algorithms that automatically deduce at compile time - without additional information from the programmer, or with partial annotations from the programmer - the type associated with a use of an object in the program.

A good number of functional programming languages allow for type inference (Haskell, OCaml, ML, etc.).

Type inference refers to the process of determining the appropriate types for expressions based on how they are used.

For example, in the expression y(4), OCaml knows that

1. y must be a function, because it is applied to something and that s.t. takes an int as input.
2. It knows nothing about the output type.

Therefore the type inference mechanism of OCaml would assign y the type int -> 'a where 'a is a type variable.

➜  apuntes-pl git:(main) ✗ ocaml
# fun y -> y(4) ;;
- : (int -> 'a) -> 'a = <fun>
# let g = fun x -> x+1;;
val g : int -> int = <fun>
# (fun y -> y(4)) g ;;
- : int = 5
# let rec rh n = if n <= 0 then "" else "hello" ^ rh (n - 1);;
val rh : int -> string = <fun>
# (fun y -> y(4)) rh ;;
- : string = "hellohellohellohello"

As an example of type inference, consider the following session in OCaml:

pl@nereida:~/src/perl/attributegrammar/Language-AttributeGrammar-0.08/examples$ ocaml
        Objective Caml version 3.09.2
 
# let minimo = fun i j -> if i<j then i else j;;
val minimo : 'a -> 'a -> 'a = <fun>
# minimo 2 3;;
- : int = 2
# minimo 4.9 5.3;;
- : float = 4.9
# minimo "hola" "mundo";;
- : string = "hola"

The OCaml compiler infers the type of the expressions.

Thus, the type associated with the function min is 'a -> 'a -> 'a, which is a type expression that contains type variables.

The operator -> is right associative, so the expression should be read as 'a -> ('a -> 'a) and not as ('a -> 'a) -> 'a.

Basically, it says: minimo is a function that takes an argument of type 'a (where 'a is a type variable that will be instantiated at the time of the function’s use) and returns a function that takes elements of type 'a and returns elements of type 'a.

Functions of Several Variables versus Functions that Return Functions

Although it might be thought that a more appropriate description of the type of the function minimo would be 'a x 'a -> 'a, the truth is that in some functional languages it is common for all functions to be considered as functions of a single variable.

The function of two variables 'a x 'a -> 'a can be seen as a function 'a -> ('a -> 'a).

Indeed, the function minimo when it receives an argument returns a function:

    # let min_mundo = minimo "mundo";;
    val min_mundo : string -> string = <fun>
    # min_mundo "pedro";;
    - : string = "mundo"
    # min_mundo "antonio";;
    - : string = "antonio"
    # min_mundo 4;;
    This expression has type int but is here used with type string
    # min_mundo(string_of_int(4));;
    - : string = "4"

This strategy of reducing functions of several variables to functions of a single variable that return functions of a single variable is known as currying or partial application.

Polimorfismo

El polimorfismo es una propiedad de ciertos lenguajes que permite una interfaz uniforme a diferentes tipos de datos.

Se conoce como función polimorfa a una función que puede ser aplicada o evaluada sobre diferentes tipos de datos.

Un tipo de datos se dice polimorfo si es un tipo de datos generalizado o no completamente especificado. Por ejemplo, una lista cuyos elementos son de cualquier tipo.

Polimorfismo Ad-hoc y polimorfismo paramétrico

Se llama Polimorfismo Ad-hoc a aquel en el que el número de combinaciones que pueden usarse es finito y las combinaciones deben ser definidas antes de su uso.

Se habla de polimorfismo paramétrico si es posible escribir el código sin mención específica de los tipos, de manera que el código puede ser usado con un número arbitrario de tipos.

Por ejemplo, la herencia y la sobrecarga de funciones y métodos son mecanismos que proveen polimorfismo ad-hoc.

Los lenguajes funcionales, como OCaml suelen proveer polimorfismo paramétrico.

En OOP el polimorfismo paramétrico suele denominarse programación genérica

En el siguiente ejemplo en OCaml construimos una función similar al map de Perl.

La función mymap ilustra el polimorfismo paramétrico:

la función puede ser usada con un número arbitrario de tipos, no hemos tenido que hacer ningún tipo de declaración explícita y sin embargo el uso incorrecto de los tipos es señalado como un error:

    # let rec mymap f list =
      match list with
          [] -> []
        | hd :: tail -> f hd :: mymap f tail;;
    val mymap : ('a -> 'b) -> 'a list -> 'b list = <fun>
    # mymap (function  n -> n*2) [1;3;5];;
    - : int list = [2; 6; 10]
    # mymap (function  n -> n.[0]) ["hola"; "mundo"];;
    - : char list = ['h'; 'm']
    # mymap (function  n -> n*2) ["hola"; "mundo"];;
    This expression has type string but is here used with type int

En los apuntes del profesor en Análisis de Tipos de Funciones Polimorfas se muestra un pequeño lenguaje que permite el polimorfismo paramétrico. Está escrito en Perl usando Eyapp. Esta es la gramática Eyapp basada en la sección A language with Polymorphic functions del libro de Aho, Sethi y Ullman, 1986, p. 367:

  p: d <+ ';'> '{' e <%name EXPS + ';'> '}'
  ;
 
  d: id ':' t
  ;
 
  t:  INT
    | STRING
    | TYPEVAR
    | LIST '(' t ')'
    | t '*' t
    | t '->' t
    | '(' t ')'
  ;
 
  e:  id '(' optargs ')'
    | id
  ;
 
  optargs:
      /* empty */
    | args
  ;
 
  args: e
     | args ',' e
  ;
 
  id: ID
  ;

Y este es un ejemplo de programa conforme a la gramática Eyapp anterior:

pl@nereida:~/doc/casiano/PLBOOK/PLBOOK/code/Aho-Polymorphism/lib/Aho/script$ \
                                                         cat -n prueba01.ply
1  first :  list(ALPHA) -> ALPHA;
2  q : list(list(int))
3  {
4    first(first(q))
5  }

Equivalencia de Expresiones de Tipo

La introducción de nombres para las expresiones de tipo introduce una ambiguedad en la interpretación de la equivalencia de tipos. Por ejemplo, dado el código:

                     typedef int v10[10];
                     v10 a;
                     int b[10];

¿Se considera que a y b tienen tipos compatibles?

Equivalencia de tipos estructural y equivalencia de tipos nominal

Si utilizamos la opción de sustituir los nombres por sus definiciones y permitimos en la definición de tipo el uso de nombres de tipo no declarados se pueden producir ciclos en el grafo de tipos.

Por ejemplo, el siguiente programa:

    nereida:~/src/perl/testing> cat -n typeequiv.c
      1  #include <stdio.h>
      2
      3  typedef struct {
      4     int x, y;
      5     struct record *next;
      6  } record;
      7
      8  record z,w;
      9
     10  struct recordcopy {
     11     int x, y;
     12     struct recordcopy *next;
     13  } r,k;
     14
     15
     16  main() {
     17    k = r; /* no produce error */
     18    z = w; /* no produce error */
     19    r = z;
     20  }

Produce el siguiente mensaje de error:

    nereida:~/src/perl/testing> gcc -fsyntax-only typeequiv.c
    typeequiv.c: En la función 'main':
    typeequiv.c:19: error: tipos incompatibles en la asignación

En lenguajes dinámicos una forma habitual de equivalencia de tipos es el tipado pato:

Duck typing

Duck typing is a form of dynamic typing where the set of methods and properties of an object determine the validity of its use. This means:

Two objects belong to the same duck type if they implement/support the same interface, regardless of whether or not they have a relationship in the inheritance hierarchy.

The term refers to the so-called duck test: If it waddles like a duck, and quacks like a duck, it’s a duck!.

Type Conversion

The type checker of a C compiler can modify the AST to introduce conversions where necessary. For example, if we have the following C program:

    int i;
    float x;
 
    x+i;

Given the expression tree PLUS(VAR, VAR), the type checker will introduce an intermediate node INT2FLOAT to indicate the need for the conversion and specify the type of PLUS being used:

                                  PLUSFLOAT(VAR, INT2FLOAT(VAR)).

An optimization tree transformation that comes into play here is the compile-time type conversion of constants. For example, given the two programs:

     float X[N];               float X[N];          
     int i;                    int i;               
                                                    
     for(i=0; i<N; i++) {      for(i=0; i<N; i++) { 
       X[i] = 1;                 X[i] = 1.0;        
     }                         }                    

The performance effects will be dire if the compiler does not perform the conversion of the integer constant 1 in the program on the left at compile time but instead leaves the conversion to a conversion subroutine that is called at runtime. In such a case, the performance of the programs on the left and right would be completely different.

References

• Apuntes del Profesor sobre Análisis de Tipos. 2000-2012.